Storing hierarchical data in a database Part 2a: Modified preorder tree traversal

Second part in this series of discussions/tutorials on storing hierarchical data in a database. You can read the first on here. The original article I read that got me started on these ideas can be found here (you’ll notice the tree diagrams are similar). Most credit should be given to Gijs Van Tulder; I simply modified some of his code and added to his explanation where appropriate.

This time we’re going to take a look at the basics of the modified preordered tree traversal algorithm.

Consider the tree used in part 1, which uses the adjacency list model:

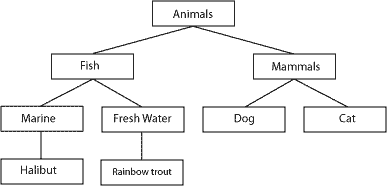
[table: animal_tree, adjacency list model]
| id  | parent_id   | name
|-----+-------------+-------------
| 1   |  0          | Animals
| 2   |  1          | Fish
| 3   |  1          | Mammals
| 4   |  2          | Marine
| 5   |  2          | Fresh Water
| 6   |  4          | Halibut
| 7   |  5          | Rainbow Trout
| 8   |  3          | Dog
| 9   |  3          | Cat
|-----+-------------+-------------

What the modified preordered method does is store the relationships between neighboring nodes in order to recreate the tree structure. We do this by storing “lft” and “rght” (“left” and “right” are reserved SQL keywords) values at each node; as you descend a tree, the left-hand values increase, and likewise, as you ascend the right-hand values increase. It’s hard to visualize until you see it in action:

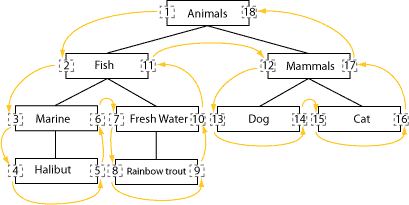
Pay special attention to the sequence in which these nodes are ordered, as shown by the arrows.

Here’s the presorted table for the above tree:

[table: animal_tree, presorted model]
| lft | rght        | name
|-----+-------------+-------------
| 1   |  18         | Animals
| 2   |  11         | Fish
| 12  |  17         | Mammals
| 3   |  6          | Marine
| 7   |  10         | Fresh Water
| 4   |  5          | Halibut
| 8   |  9          | Rainbow Trout
| 13  |  14         | Dog
| 15  |  16         | Cat
|-----+-------------+-------------

…and one of the first things you probably want to do with your new presorted data? Create a tree. First things first, though. The code behind it is more difficult to understand than the adjacency model but the overhead is greatly reduced because you only need two queries for to retrieve tree information from the database (adjacency uses a new query every time you recursively enter the retrieve function).

In its simplest form the queries are:
(retrieves the left and right values for the starting node)
SELECT lft,rght FROM animal_tree WHERE name="$name";
SELECT * FROM animal_tree WHERE lft BETWEEN $row['lft'] AND $row['right'] ORDER BY lft ASC;…and that’s it.

Take a look at the code (modified from the example in the Sitepoint article):

//I use my own database classes, but it should be easy enough to follow what's happening.
function get_tree($name="Animal",&$DB) {

$result=$DB->query("SELECT lft,rght FROM animal_tree WHERE name="$name"");
$row=$DB->fetchRow($result);
$result2=$DB->query("SELECT * FROM animal_tree WHERE lft BETWEEN {$row['lft']} AND {$row['rght']} ORDER BY lft ASC");

$right = array();

$row=$DB->fetchAssoc($result2);

$ii=0; //start counter at 0
foreach($row as $row) {
if(count($right)>0) {

/* $right[max#] is the last array element, which holds the
* rght value from the previous row, which is a parent in
* many cases, but if not a parent, it keeps popping-off
* the last element of the $right array - going back up
* the tree until $row[right] (current node) finds its
* parent (the parents rght value is greater than the
* child's rght)
*/
while($right[count($right)-1]$value)
{
print(str_repeat(' ',$value['indent'])."({$value['lft']})".$value['node']."({$value['right']})n");
}
}


…and in-case you want the path to a particular node:
SELECT * FROM animal_tree WHERE lft$rght ORDER BY lft ASC

..to count the number of descendants: $d=(rght-lft-1)/2

Thanks, again to Gijs for the excellent tutorial. Next time we will explore some ways to modify and manipulate the tree.